SPECTRALE (THÉORIE)

SPECTRALE (THÉORIE)

L’objet de la théorie spectrale est d’obtenir, pour certains endomorphismes d’un espace hilbertien, des formes réduites analogues aux formes canoniques de Jordan pour les endomorphismes d’un espace vectoriel de dimension finie et aux formes diagonales pour les endomorphismes hermitiens d’un espace vectoriel hermitien de dimension finie. La théorie des applications de Hilbert-Schmidt, rencontrées pour la première fois à propos des équations intégrales, permet de construire une première généralisation des résultats obtenus en dimension finie. En fait, le cadre naturel de cette généralisation est celui des applications compactes, étudiées par F. Riesz.

Néanmoins, le cas des endomorphismes les plus généraux échappe à ce cadre; il fait l’objet de la théorie spectrale de Hilbert, qui utilise les techniques de l’intégration. On a axiomatisé la théorie spectrale, grâce aux concepts généraux de C-algèbre et d’algèbre hilbertienne.

1. Théorie spectrale algébrique

Tant en algèbre qu’en analyse, on est fréquemment amené à définir et à calculer des fonctions d’un endomorphisme u d’un espace vectoriel E sur un corps commutatif K (inverse, puissances, exponentielle, etc.). À cet effet, il est utile de chercher les droites de E stables par u . On est ainsi conduit aux notions de valeur propre et de vecteur propre. On dit qu’un élément non nul x de E est un vecteur propre de u si la droite engendrée par x est stable par u , c’est-à-dire s’il existe un élément de K tel que u (x ) =x . On dit qu’un scalaire est une valeur propre de u si le noyau de u 漣I^E est non réduit à0. L’ensemble des valeurs propres de u s’appelle spectre ponctuel de u et se note sp (u ).

Même lorsque E est de dimension finie et que K est algébriquement clos, il peut arriver que E ne soit pas somme directe de droites stables par u . C’est le cas par exemple lorsque u est un endomorphisme nilpotent non nul de E. On voit apparaître l’intérêt de la notion d’endomorphisme diagonalisable : on appelle ainsi un endomorphisme u de E tel que E soit somme directe de droites stables par u , ou encore tel qu’il existe une base de E constituée de vecteurs propres de u . Lorsque E est de dimension finie, cela revient à dire qu’il existe une base de E telle que la matrice associée à u dans cette base soit diagonale. Il peut arriver que plusieurs droites stables correspondent à une même valeur propre.

C’est pour cela que, pour toute valeur propre de u , on introduit le sous-espace propre associé à, à savoir le noyau de u 漣I^E. La somme des sous-espaces propres de u est toujours directe; pour que u soit diagonalisable, il faut et il suffit que cette somme soit égale à E.

Dans le cas où u n’est pas diagonalisable, il convient d’introduire des sous-espaces vectoriels de E stables par u «plus gros» que les sous-espaces propres: on appelle sous-espace spectral de u associé à une valeur propre de u le sous-espace vectoriel F size=1^凞 réunion des sous-espaces vectoriels:

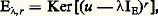où r 捻 N. Si la suite (E size=1^凞,r ) est stationnaire, on dit que est l’indice fini. Le plus petit des entiers r tels que E size=1^凞,r = F size=1^凞 s’appelle alors indice de et se note n (). Lorsque F size=1^凞 est de dimension finie, on dit que est de multiplicité finie; la dimension de F size=1^凞 s’appelle alors multiplicité de la valeur propre. La somme des sous-espaces spectraux de u est toujours directe; on dit que u est trigonalisable si cette somme est égale à E.

Lorsque E est de dimension finie, le spectre de u est fini; il est constitué des scalaires tels que:

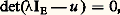c’est-à-dire des racines du polynôme det (XI^E 漣 u ), appelé polynôme caractéristique de u . De plus, toute valeur propre de u est de multiplicité finie et égale à la multiplicité de la racine du polynôme caractéristique de u . En outre, l’idéal de K[X] constitué des polynômes P tels que P(u ) = 0 est non réduit à0; il admet donc un générateur, appelé polynôme minimal de u . Toute valeur propre de u est d’indice fini et égal à la multiplicité de la racine du polynôme minimal de u . Enfin, le polynôme minimal de u divise le polynôme caractéristique de u ; ce résultat s’appelle théorème de Hamilton-Cayley .

Grâce à ces notions, on peut caractériser les endomorphismes diagonalisables et les endomorphismes trigonalisables. Pour que u soit trigonalisable, il faut et il suffit que le polynôme minimal (ou le polynôme caractéristique) de u soit scindé, c’est-à-dire décomposable en produit de facteurs du premier degré. Pour que u soit diagonalisable, il faut et il suffit que le polynôme minimal de u soit scindé et que toutes ses racines soient simples. D’autre part, pour que u soit trigonalisable, il faut et il suffit qu’il existe une base de E telle que la matrice associée à u dans cette base soit trigonale supérieure.

En combinant les caractérisations données ci-dessus, on obtient un résultat plus précis: soit u un endomorphisme trigonalisable; pour toute valeur propre de u , il existe une base B size=1^凞 du sous-espace spectral F size=1^凞 telle que la matrice associée dans cette base à l’endomorphisme u size=1^凞 de F size=1^凞 coïncidant avec u soit de la forme:

La matrice R associée à u dans la base B obtenue en réunissant les bases B size=1^凞 est une matrice diagonale de matrices trigonales:

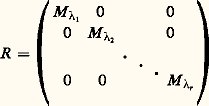Une telle matrice trigonale supérieure est dite réduite .

On peut enfin mettre la matrice associée à un endomorphisme trigonalisable sous une forme canonique, grâce à la notion matrice de Jordan ; on appelle ainsi une matrice carrée de la forme:

c’est-à-dire une matrice dont les éléments diagonaux sont égaux, dont les éléments juste au-dessus de la diagonale sont égaux à 1 et dont les autres éléments sont nuls.

Pour toute valeur propre de l’endomorphisme trigonalisable u , il existe une base B size=1^凞 de F size=1^凞 telle que la matrice M size=1^凞 associée à u size=1^凞 dans cette base soit une matrice diagonale de matrices de Jordan. La matrice J associée à u dans la base B est encore une matrice diagonale de matrices de Jordan; en particulier, ses éléments juste au-dessus de la diagonale sont égaux à 0 ou à 1. Une telle matrice est dite forme réduite de Jordan . Le calcul des puissances successives de J s’effectue aisément à partir de la formule du binôme de Newton.

Soit par exemple u l’endomorphisme de R⁵ canoniquement associé à la matrice: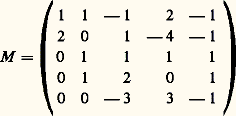

Le polynôme caractéristique de u est (X + 1)²(X 漣 1)³. L’endomorphisme u est trigonalisable, mais il n’est pas diagonalisable. Soit B la base de R⁵ définie à partir de la base canonique par la matrice de passage: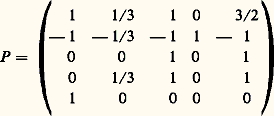

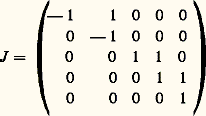La matrice J = P ^-1 MP associée à u dans la base B est sous la forme réduite de Jordan:

2. Théorie de Riesz des applications linéaires compactes

Applications linéaires compactes

Historiquement, la notion d’application linéaire compacte s’est introduite sous le nom d’application complètement continue: étant donné deux espaces vectoriels normés E et F, une application linéaire u de E dans F est dite complètement continue si de toute suite bornée (xⁿ ) d’éléments de E on peut extraire une suite (y^p ) telle que la suite (u (y^p )) soit convergente dans F.

F. Riesz fut le premier à remarquer que cette condition permet de retrouver tous les résultats de la théorie de Fredholm (cf. équations INTÉGRALES, chap. 5). En utilisant la caractérisation des espaces métriques compacts à l’aide de la condition de Bolzano-Weierstrass, on voit immédialement qu’une application linéaire u de E dans F est complètement continue si et seulement si l’image par u de la boule unité de E est une partie relativement compacte de F. Sous cette forme, la notion d’application complètement continue peut se généraliser aux espaces vectoriels topologiques.

Plus précisément, soit E et F deux espaces vectoriels topologiques localement convexes séparés. On dit qu’une application linéaire u de E dans F est compacte (resp. précompacte ) s’il existe un voisinage V de 0 dans E tel que u (V) soit une partie relativement compacte (resp. précompacte) de F.

Toute application compacte est précompacte; la réciproque est vraie si l’espace vectoriel F est complet ou, plus généralement, si toute partie fermée bornée de F est complète. Toute application précompacte est continue; la réciproque est fausse. Ainsi, pour que l’application identique I^E de E soit précompacte, il faut et il suffit que E soit de dimension finie, auquel cas elle est compacte (lemme de F. Riesz).

Les applications compactes de E dans F constituent un sous-espace vectoriel de l’espace vectoriel des applications linéaires continues de E dans F.

Soit u une application linéaire continue de E dans F et v une application linéaire continue de F dans un troisième espace G. Si l’une des applications u et v est compacte, il en est de même de l’application composée v 獵 u . En particulier, les endomorphismes compacts de E constituent un idéal bilatère de l’algèbre 硫(E) des endomorphismes continus de E.

Soit E et F les duaux topologiques de E et de F, munis de la topologie de la convergence uniforme sur les disques compacts. Alors, si u est compact, il en est de même de ^t u .

Enfin, toute application linéaire de rang fini est compacte.

On peut énoncer des propriétés analogues pour les applications précompactes.

Revenons au cas particulier où les espaces E et F sont normés; munissons l’espace vectoriel 硫(E, F) de la norme des applications linéaires continues, à savoir la norme de la convergence uniforme sur la boule unité de E. Alors les applications précompactes de E dans F constituent un sous-espace vectoriel fermé de 硫(E, F). Il en est de même des applications compactes de E dans F, lorsque F est complet. Il en résulte que la limite en norme d’une suite d’applications de rang fini est une application compacte. Réciproquement, lorsque l’espace vectoriel F est hilbertien, toute application compacte de E dans F est limite d’une suite d’applications de rang fini. Lorsque F est un espace de Banach, cette réciproque se ramène au problème suivant: l’application identique d’un espace de Banach est-elle limite forte de projecteurs de rang fini (propriété d’approximation)? Ces deux problèmes ont été résolus par la négative en 1976.

Supposons maintenant que E et F sont des espaces de Banach; soit E et F les duaux topologiques de E et de F, munis des normes correspondantes. Pour qu’une application linéaire continue u de E dans F soit compacte, il faut et il suffit que sa transposée ^tu soit une application compacte de F dans E .

En particulier, si E et F sont des espaces hilbertiens, l’adjointe u d’une application compacte u de E dans F est une application compacte de F dans E.

Les propriétés des applications de rang fini se généralisent aux applications linéaires compactes, ce qui fait le principal intérêt de ces dernières. Laurent Schwartz a dégagé le résultat fondamental suivant:

Théorème de finitude . Soit E et F deux espaces vectoriels localement convexes séparés, u et v deux applications linéaires continues de E dans F. On suppose que u est un isomorphisme de E sur F et que v est compacte. Alors le noyau de w = u + v est de dimension finie, l’image de w est un sous-espace vectoriel fermé de codimension finie dans F, et on a la formule:

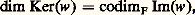dite formule du rang. De plus, w est un morphisme strict, c’est-à-dire que w définit un isomorphisme de E/Ker(w ) sur Im(w ).

Ce théorème a trouvé des applications non seulement dans la théorie spectrale, que nous esquissons ci-dessous, mais aussi dans la théorie des faisceaux analytiques cohérents (cf. FONCTIONS ANALYTIQUES - Fonctions analytiques de plusieurs variables complexes, GÉOMÉTRIE ALGÉBRIQUE, chap. 6) et dans celle des indices topologiques (cf. TOPOLOGIE - Topologie algébrique).

Spectre d’un endomorphisme compact

Examinons maintenant le cas particulier où E = F et supposons que le corps de base est le corps C des nombres complexes. On appelle spectre d’un endomorphisme continu u de E l’ensemble, noté sp(u ), des nombres complexes tels que u 漣I^E ne soit pas inversible dans l’algèbre unitaire 硫(E). Les éléments de sp(u ) s’appellent valeurs spectrales de u . Lorsque E est un espace de Banach, le spectre de u est une partie compacte non vide de C (cf. algèbres NORMÉES). Toute valeur propre de u est une valeur spectrale de u , mais la réciproque est fausse si E n’est pas de dimension finie; il peut même arriver que u n’ait aucune valeur propre. C’est la principale raison pour laquelle la réduction des endomorphismes continus de E nécessite des outils radicalement nouveaux (cf. infra , chap. 3). Cependant, lorsque l’endomorphisme u est compact, les principaux résultats de la réduction des endomorphismes d’un espace vectoriel de dimension finie se généralisent.

Plus précisément, soit u un endomorphisme compact d’un espace vectoriel localement convexe séparé E et une valeur spectrale non nulle de u .

a ) Le nombre complexe est une valeur propre de u .

b ) Le sous-espace propre:

est de dimension finie. Plus généralement, pour tout entier naturel non nul r , le sous-espace: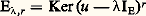

est de dimension finie. En outre, est une valeur propre d’indice fini. En particulier, le sous-espace spectral F size=1^凞 est de dimension finie.

c ) Le sous-espace vectoriel:

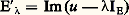est fermé de codimension finie dans E. Plus généralement, pour tout entier naturel non nul r ,

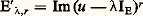est fermé de codimension finie. Il en est de même de:

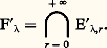d ) Les sous-espaces vectoriels F size=1^凞 et F size=1^凞 sont supplémentaires topologiques dans E (c’est-à-dire qu’ils sont supplémentaires et que les projecteurs associés sont continus). De plus, l’endomorphisme de F size=1^凞 coïncidant avec u est nilpotent, tandis que l’endomorphisme de F size=1^凞 coïncidant avec u est un automorphisme de l’espace vectoriel localement convexe séparé F size=1^凞.

En outre, le spectre d’un endomorphisme compact u d’un espace vectoriel localement convexe séparé E est une partie compacte non vide de C, et tout point de sp(u ) autre que 0 est isolé. Autrement dit, ou bien le spectre de u est fini, ou bien il est constitué de 0 et d’une suite (ⁿ ) de nombres complexes non nuls convergeant vers 0. Lorsque l’espace vectoriel E n’est pas de dimension finie, 0 appartient toujours au spectre de u . On notera néanmoins que les résultats précédents ne s’appliquent pas à la valeur spectrale 0. Or, il peut arriver que u soit compact et injectif et que le spectre de u soit réduit à0, ce qui signifie que u est quasi nilpotent, c’est-à-dire que:

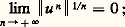c’est le cas pour l’endomorphisme de 暈([0, 1]) qui à toute fonction continue sur [a , b ] associe sa primitive s’annulant au point a .

Enfin, l’endomorphisme transposé ^t u d’un endomorphisme compact u a le même spectre que u et les mêmes valeurs propres non nulles, avec les mêmes indices et les mêmes multiplicités pour u et ^tu . Plus précisément, pour tout entier naturel non nul r , le sous-espace:

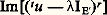est l’orthogonal de Ker[(u 漣I^E)^r ] et de même le sous-espace:

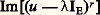est l’orthogonal de Ker[(^tu 漣I^E size=1)^r ].

Alternative de Fredholm

Soit E un espace vectoriel de dimension finie, E son dual, w un endomorphisme de E et ^tw le transposé de w . Alors l’alternative suivante est vraie (cf. algèbre LINÉAIRE ET MULTILINÉAIRE):

a ) Ou bien w et ^tw sont des automorphismes. Dans ce cas, pour tout élément y de E et pour tout élément y de E, les deux équations suivantes:

admettent une solution et une seule.

b ) Ou bien les noyaux de w et de ^tw ne sont pas réduits à0 et, dans ce cas,

L’équation (1) admet une solution si et seulement si y est orthogonal à Ker(^tw ), et l’équation (2) admet une solution si et seulement si y est orthogonal à Ker(w ).

Cette alternative ne subsiste pas lorsque w est un endomorphisme continu d’un espace vectoriel localement convexe séparé E, même si E est un espace hilbertien et si w est hermitien. Néanmoins, à l’aide du théorème de finitude et de la théorie de Riesz, on démontre l’énoncé suivant:

Soit E un espace vectoriel localement convexe séparé, E son dual topologique, u un automorphisme de E, v un endomorphisme compact de E et w = u + v . Alors l’alternative énoncée plus haut reste valable, mutatis mutandis . En particulier, les assertions suivantes sont équivalentes:

a ) l’endomorphisme w est un automorphisme de E;

b ) l’endomorphisme w est injectif;

c ) l’endomorphisme w est surjectif;

d ) l’endomorphisme ^tw est un automorphisme de E ;

e ) l’endomorphisme ^tw est surjectif;

f ) l’endomorphisme ^tw est injectif.

Grâce aux résultats précédents, on peut préciser la nature de la résolvante d’un endomorphisme compact . Soit u un endomorphisme d’un espace vectoriel localement convexe séparé E. On dit qu’un nombre complexe est une valeur singulière de u si n’est pas seul et si 1/ appartient à sp(u ). Le complémentaire de l’ensemble des valeurs singulières est noté reg(u ). Lorsque u est compact, reg(u ) est un ouvert de C dont le complémentaire est discret. Considérons alors la résolvante R de u , c’est-à-dire l’application: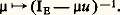

Cette résolvante est holomorphe sur reg (u ), et chaque valeur singulière de u est un pôle d’ordre égal à la multiplicité m () de la valeur propre 1/. Plus précisément, soit p size=1^凞 et q size=1^凞 les projecteurs sur F size=1^益 et F size=1^益, où 益 = 1/. Alors u se décompose de la manière suivante:

où r size=1^凞 = q size=1^凞u et s size=1^凞 = p size=1^凞u . De plus:

a ) L’endomorphisme r size=1^凞 est compact et est une valeur régulière de r size=1^凞.

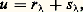b ) L’endomorphisme s size=1^凞 est continu de rang fini et est l’unique valeur singulière de s size=1^凞.

c ) La résolvante de u est égale au produit des résolvantes de r size=1^凞 et de s size=1^凞. Celle de r size=1^凞 est holomorphe au voisinage de; celle de s size=1^凞 admet pour unique pôle, d’ordre m ().

Cas des espaces hilbertiens

Soit E un espace hilbertien et u un endomorphisme continu de E. Supposons que u est normal, c’est-à-dire que u u = uu (l’importance de cette classe d’endomorphismes provient du fait que les endomorphismes hermitiens, antihermitiens ou unitaires sont normaux). Alors la norme de u est égale au rayon spectral de u , c’est-à-dire au rayon du plus petit disque de centre 0 contenant le spectre de u (cf. algèbres NORMÉES). En particulier, un endomorphisme normal dont le spectre est réduit à0 est nul. En outre, toute valeur propre de u est d’indice 1, et l’on a:

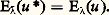Enfin, les sous-espaces propres de u sont orthogonaux deux à deux. Néanmoins, il peut arriver qu’un endomorphisme continu normal (ou même hermitien) n’admette aucune valeur propre. Il en est ainsi de l’endomorphisme de multiplication par une fonction continue non constante à valeurs réelles dans l’espace hilbertien L²([a , b ]) des classes de fonctions de carré intégrable sur [a , b ]. Toutefois, lorsque u est à la fois compact et normal, la théorie de Riesz prend la forme achevée que voici:

Théorème spectral . Soit u un endomorphisme compact et normal d’un espace hilbertien E.

a ) Le spectre de u est une partie compacte de C dont tout point autre que 0 est isolé.

b ) Toute valeur spectrale non nulle de u est valeur propre de u .

c ) Pour tout élément non nul de sp(u ), le sous-espace propre E size=1^凞 est de dimension finie.

d ) L’espace hilbertien E est somme hilbertienne des sous-espaces propres de u , c’est-à-dire que ces sous-espaces propres sont orthogonaux deux à deux et que leur somme directe est dense dans E. En particulier, tout vecteur x de E s’écrit d’une manière et d’une seule sous la forme:

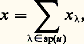où, pour tout élément de sp(u ), x size=1^凞 appartient à E size=1^凞. Dans ces conditions, on a les formules:

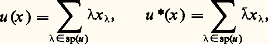dites formules de décomposition spectrale . Il existe donc une base hilbertienne de E constituée de vecteurs propres de u .

On notera que le théorème précédent s’applique au cas d’un endomorphisme normal u d’un espace vectoriel hermitien de dimension finie. Dans ce cas, le spectre de u est fini, et les familles sommables intervenant dans les formules de décomposition spectrale se réduisent à des sommes finies. Il existe alors une base orthonormale de E constituée de vecteurs propres de u . En particulier, tout endomorphisme normal de E est diagonalisable. Par suite, pour toute matrice normale M , il existe une matrice diagonale D et une matrice unitaire P telles que:

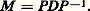Ce résultat s’applique à la réduction des formes hermitiennes par rapport à une forme hermitienne positive non dégénérée (cf. formes QUADRATIQUES).

La théorie précédente s’applique aussi au cas des endomorphismes de puissance p -ième nucléaire: étant donné un espace hilbertien E et un endomorphisme hermitien positif h , le nombre:

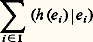est indépendant du choix d’une base hilbertienne (eⁱ ), i 捻 I, de E. Ce nombre s’appelle trace de h et se note tr(h ). Soit maintenant p un nombre réel supérieur à 1, E et F deux espaces hilbertiens et u un élément de 硫(E, F). On appelle valeur absolue de u l’endomorphisme | u | = (u u )^1/2; on dit que u est de puissance p -ième nucléaire si la trace de | u | ^p est finie. On pose alors:

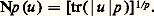Lorsque p = 1, de telles applications sont dites nucléaires , ou encore traçables . Lorsque p = 2, on les appelle applications de Hilbert-Schmidt , ou applications de carré traçable (cf. équations DIFFÉRENTIELLES, chap. 3, et équations INTÉGRALES, chap. 5). Les applications de puissance p -ième nucléaire sont compactes; plus précisément, soit u une application compacte de E dans F, soit (eⁱ ), i 捻 I, une base hilbertienne de E constituée de vecteurs propres de | u | , et ( 猪ⁱ ), i 捻 I, la famille correspondante de valeurs propres. Pour que u soit de puissance p -ième nucléaire, il faut et il suffit que:

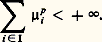Dans ces conditions, on a:

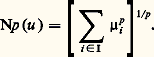Les applications de puissance p -ième nucléaire constituent un sous-espace vectoriel, noté 硫^p (E, F), de l’espace vectoriel des applications compactes, et l’application u 料 N^p (u ) est une norme sur 硫^p (E, F), qui en fait un espace de Banach. Les applications de rang fini sont denses dans 硫^p (E, F), et la convergence au sens de la norme N implique la convergence dans 硫(E, F). On peut alors développer une théorie des espaces 硫^p (E, F) en tous points analogues à celle des espaces L^p intervenant dans la théorie de l’intégration (cf. INTÉGRATION ET MESURE, chap. 4).

Soit maintenant u un élément de 硫¹(E) et (ⁿ ) la suite des valeurs propres non nulles de u , chacune d’elles étant écrite un nombre de fois égal à sa multiplicité. La série de terme général (ⁿ ) est absolument convergente, et donc convergente; sa somme s’appelle trace de u . De même, pour tout nombre complexe z , le produit infini de terme général (1 + zⁿ ) est convergent; on pose:

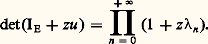La fonction entière z 料 det(I^E + zu ) s’appelle déterminant de Fredholm de l’endomorphisme u ; on peut calculer son développement en série entière en introduisant les puissances extérieures hilbertiennes de u , notées 炙^r (u ):

On généralise ainsi la théorie du polynôme caractéristique, ce qui constitue la théorie de Fredholm .

3. Théorie spectrale de Hilbert

Soit u un endomorphisme continu normal d’un espace hilbertien E. La sous-algèbre unitaire fermée autoadjointe A de 硫(E) engendrée par u est une C-algèbre commutative unitaire, dont le spectre s’identifie canoniquement à celui de u (cf. algèbres NORMÉES). De plus, la transformation de Gelfand est un isomorphisme de A sur l’algèbre 暈(sp(A)) des fonctions continues sur le spectre de A. L’isomorphisme réciproque définit un morphisme 﨏 de 暈(sp(A)) dans l’algèbre unitaire 硫(E); c’est l’unique morphisme de 暈(sp(A)) dans 硫(E) tel que 﨏(z ) =u , où z est l’injection canonique de sp (A) dans C. Pour tout élément f de 暈(sp (A)), l’endomorphisme 﨏(f ) se note encore f (u ). Cette théorie permet donc de définir un calcul fonctionnel portant sur les fonctions continues de u . En particulier, u = 﨏( 磻 ). L’objet de la théorie spectrale de Hilbert est d’étendre le calcul fonctionnel à des fonctions plus générales. On observe à cet effet que, pour tout couple (x , y ) d’éléments de E, l’application:

est (cf. INTÉGRATION ET MESURE, chap. 4) une mesure de Radon sur sp(u ). De plus, l’application:

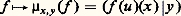
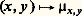est sesquilinéaire hermitienne. Enfin, on a:

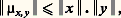Les mesures 猪^x,y s’appellent mesures spectrales associées à u . On dit qu’une fonction f définie sur sp(u ) à valeurs complexes est u -mesurable si, pour tout couple (x , y ) d’éléments de E, cette fonction est 猪^x,y -mesurable. On note L size=1^秊(u ) l’algèbre des classes de fonctions u -mesurables essentiellement bornées et, pour tout nombre réel p 閭 1, on note L^p (u ) l’espace vectoriel des classes de fonctions u -mesurables appartenant à L^p ( 猪^x,y ) pour tout couple (x , y ) d’éléments de E. On démontre alors le théorème fondamental suivant: Pour tout élément f de L¹(u ), il existe un élément et un seul de 硫(E), noté f (u ), tel que, pour tout couple (x , y ) d’éléments de E, on ait:

C’est pourquoi f (u ) se note encore:

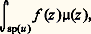où 猪 désigne la mesure vectorielle correspondant aux mesures scalaires 猪^x,y . En particulier, on a les formules de décomposition spectrale suivantes:

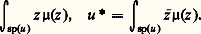De plus, l’application f 料 f (u ) est linéaire, et [f (u )] = 肋 (u ). En outre, pour toute suite (fⁿ ) d’éléments de L¹(u ) convergeant simplement vers f , dominée par une fonction positive g appartenant à L¹(u ), la fonction f appartient à L¹(u ) et les endomorphismes fⁿ (u ) convergent fortement vers f (u ); c’est le théorème de convergence dominée de Lebesgue . Enfin, pour tout élément f de L¹(u ) et pour tout élément g de L size=1^秊(u ), on a l’égalité:

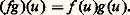En particulier, l’application u 料 f (u ) définit un morphisme de la C-algèbre L size=1^秊(u ) dans 硫(E), prolongeant ainsi le calcul fonctionnel aux éléments de L size=1^秊(u ); les éléments f (u ), où f appartient à L¹(u ), appartiennent au bicommutant de A. Lorsque f est la fonction caractéristique d’une partie M de sp(u ), f ( 﨑^M) est un projecteur hermitien de E, noté P^M, appartenant au bicommutant de A. Les projecteurs P^M s’appellent projecteurs spectraux de u , et leurs images s’appellent variétés spectrales de u . Lorsque E est de dimension finie et que M est réduite à un point, on retrouve la notion de sous-espace propre. Le calcul fonctionnel précédent permet de généraliser aux endomorphismes normaux la plupart des résultats de la théorie spectrale classique. On peut même définir un calcul fonctionnel portant sur les opérateurs normaux non bornés; ses applications sont nombreuses (mécanique quantique, problèmes de Sturm-Liouville).

Encyclopédie Universelle. 2012.